luar yang bekerja pada simpul itu, dan gaya dalam (gaya batang) yang timbul di titik itu. Gaya luar dan gaya batang berpotongan di titik simpul, maka untuk menghitung gaya-gaya yang belum diketahui digunakan
persamaan ΣV = 0 dan ΣH = 0.
Dari dua persamaan di atas, maka pada tiap-tiap simpul yang akan dicari gaya batangnya harus hanya 2 (dua) atau 1 (satu) batang yang belum diketahui dan dianggap sebagai batang tarik (meninggalkan simpul).
Gaya-gaya batang yang sudah diketahui, bila batang tarik arahnya meninggalkan simpul, dan bila batang tekan arahnya menuju simpul. Jadi tiap-tiap titik simpul dapat dicari keseimbangannya satu demi satu, sehingga seluruh konstruksi dapat diketahui gaya-gaya batangnya. Sebagai contoh konstruksi rangka batang kuda-kuda seperti pada gambar di bawah ini, akan dicari gaya-gaya batangnya.
Terlebih dahulu tentukan kestabilan konstruksi, dengan menggunakan persamaan : 2s – m – r = 0, dimana diketahui; s = 4, m = 5, r = 3 (sendi 2 bilangan reaksi + rol 1 bilangan reaksi), maka diperoleh:
2.4 – 5 – 3 = 0, jadi konstruksi stabil. Begitu juga reaksi perletakan, tentukan secara analitis dengan menggunakan keseimbangan momen pada salah satu titik tumpuan.
Untuk menentukan gaya-gaya batang, diawali dengan meninjau simpul A, ada gaya reaksi VA sudah diketahui yang arahnya menuju simpul, dan ada dua batang yang gaya batangnya belum diketahui, yaitu gaya batang 1 dan 4 yang dimisalkan b1 dan b4, maka kedua batangnya dianggap tarik dengan arah meninggalkan simpul A.
Tanda b4 adalah negatif, berarti batang tekan (menuju simpul), dan tanda b1 adalah positif, berarti batang tarik (meninggalkan simpul). Setelah itu tinjau simpul C, ada gaya 2P dan gaya batang b1 sudah diketahui, keduanya mempunyai arah meninggalkan simpul, dan ada dua batang yang gaya batangnya belum diketahui, yaitu gaya batang 5 dan 2 yang dimisalkan b5 dan b2, maka kedua batangnya dianggap tarik dengan arah meninggalkan simpul C.
Tanda b5 dan b2 adalah positif, berarti batang tarik (meninggalkan simpul). Selanjutnya tinjau simpul D, ada gaya batang b5 dan b4 sudah diketahui, dengan arah b5 meninggalkan simpul dan b4 menuju simpul, dan ada satu batang yang gaya batangnya belum diketahui, yaitu gaya batang 3 yang dimisalkan b3, maka batangnya dianggap tarik dengan arah meninggalkan simpul D.
Tanda b3 adalah negatif, berarti batang tekan (menuju simpul). Semua batang gaya batangnya sudah diketahui, namun untuk membuktikan keseimbangan pada semua titik simpul, perlu ditinjau simpul B, ada gaya reaksi VB yang arahnya menuju simpul, gaya batang b2 arahnya meninggalkan simpul, dan gaya batang b3 arahnya menuju simpul.
Dari persamaan keseimbangan gaya vertikal dan horisontal, terbukti bahwa gaya-gaya batang pada simpul B sudah seimbang. Setelah semua titik keseimbangan ditinjau dapat diringkaskan besarnya gaya batang seluruh rangka seperti terlihat dalam tabel di bawah ini.
Tabel Daftar Gaya-Gaya Batang Contoh Rangka Batang Kuda-Kuda


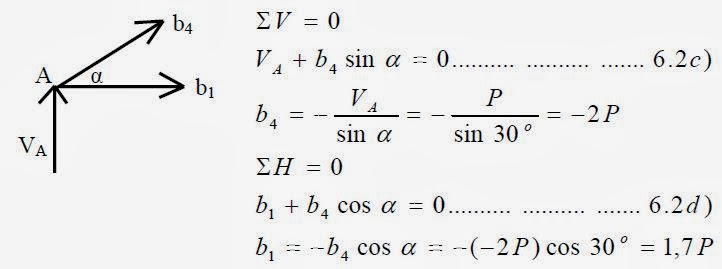




Tidak ada komentar:
Posting Komentar